Este post es una respuesta al reto MDUG del espirógrafo. El día 18 de Enero se reúne el grupo de usuarios de Dynamo de Madrid.
El caso es que lanzan el siguiente reto que podéis consultar en su página web, a la que podéis acceder haciendo click en la imagen:

El caso es que, no sé por qué, no me dejaba registrarme… y yo quería contestar antes de marchar esta tarde a comerme el roscón de reyes, sí… este post lo estoy escribiendo un día 5 de Enero por la tarde aunque se publicará el martes que viene, así que dejo os voy a dejar aquí mi explicación.
PASO 1. Aproximación.

El dynamo está resuelto con todas las explicaciones paso a paso de su desarrollo, que os dejo en este mismo link.
¡Hay que ser ordenados a la hora de hacer un dynamo o nadie sabrá qué estamos haciendo! Aunque ese es un asunto que trataremos en próximos posts.
Ahora bien, este primer avance es sólo una simplificación y os preguntaréis, ¿comorrr?
Sí, efectivamente, es una simplificación ya que solo sería válido si la curva que genera una circunferencia al desplazarse rotando sobre su lado fuera otro arco de circunferencia pero… esto no es así. La curva que genera este movimiento es una cicloide, así que el primer tanteo nos vale como aproximación pero no está exacto. Así que, como decían en cifras y letras, ¡vamos a por el exacto!
PASO 2. Exacto.
Habrá mil formas de resolver este mismo ejercicio, yo os cuento una. En este caso parto de algo muy simple y es que el ángulo de cualquier arco de circunferencia es igual a la longitud que recorre entre el radio.
ángulo circ = long que recorre / radio
¡ojo, en radianes!
Con este dato lo que hago es dividir la curva en muchos trozos y, en cada trozo, obtener la distancia que habría recorrido la circunferencia en ese punto. Con esta distancia y, conociendo el dato del radio, puedo calcular el giro que ha recorrido la circunferencia en cada punto.
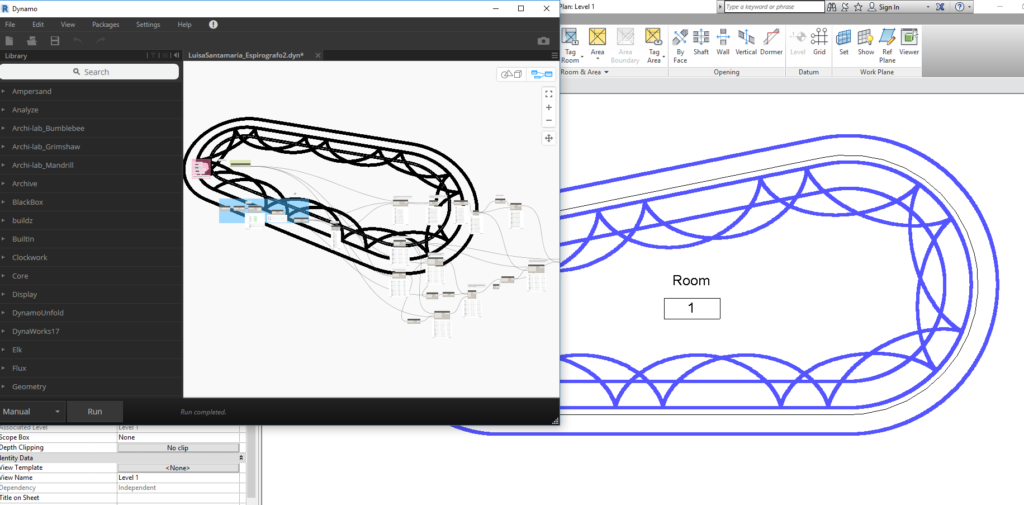
Una vez obtenido este giro y su ángulo trazo desde cada punto una perpendicular a la curva que cierra la habitación. Después giro cada punto el ángulo necesario. Esto es solo válido para la primera vuelta que hacemos a la curva. Para la segunda vuelta tendríamos que sumar al ángulo de inicio el ángulo recorrido con el que terminamos la primera vuelta y así para los sucesivos recorridos de la curva. Podéis acceder al desarrollo del Dynamo haciendo click en la imagen.
Ah, y también os dejo aquí el link a la solución exacta.
Aquí tenéis cómo se podría seguir la iteración, este dynamo completo está subido a la web de MDUG y aquí.
Así quedaría en Revit este espirógrafo:
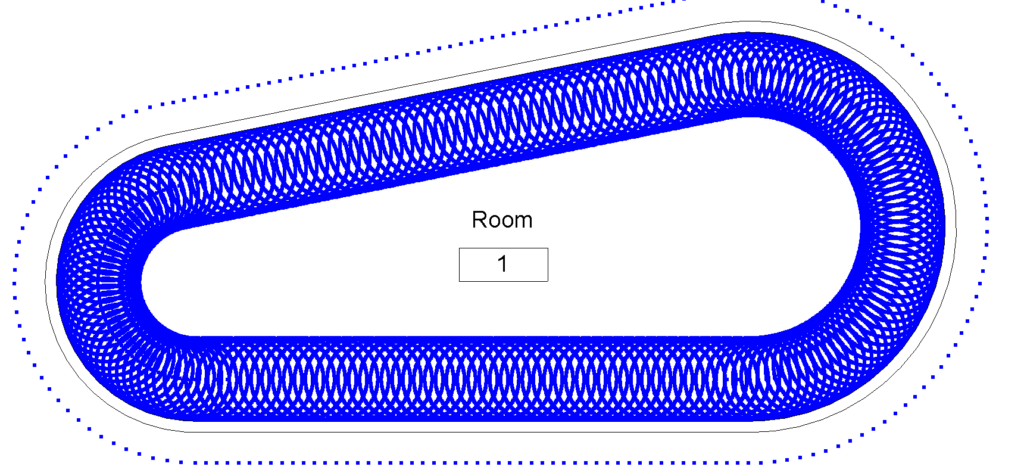
Lo bonito sería, al final, hacer las iteraciones con python. Si tengo tiempo antes del MDUG lo incorporaré al post.
Paso 3. Esto ya como curiosidad
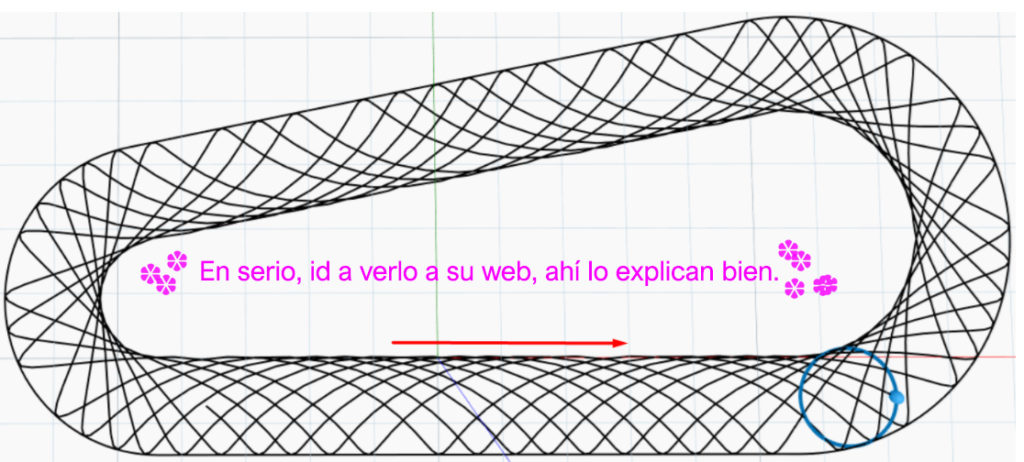
Una cosa divertida. Si le damos la vuelta a los ángulos de nuestra esfera, es decir, calculamos bien los grados pero mal el sentido de giro… ¡atención navegantes zurdos! tendríamos algo como esto:
Esto último es que me ha parecido bonito de forma y una curiosidad chula.
¡Un saludo y mucho BIM!
ojoojojo: Yo no estoy recogiendo soluciones así que: ¡no me las mandéis a mí! Es en la página de MDUG donde tenéis que subirlas. Repito su web: http://www.dynamomadrid.org
PD. Los lectores habéis hecho un trabajazo con este artículo y me habéis mandado posibles mejoras y excepciones. Franxo de Modelical, por ejemplo, me decía que «mi definición no valía para una habitación de forma cuadrangular». ¡Mil gracias! el artículo del 23 de Enero irá de «purgado de errores en Dynamo» y os contaré el proceso de purgado. Gracias a todos.
![]() Reto de programación en Dynamo por Especialista3D está licenciado bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Reto de programación en Dynamo por Especialista3D está licenciado bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.